Поскольку в модели Био интерес представляют не абсолютные значения искомых функций, а их приращения за время t действия внешней нагрузки, все уравнения в дальнейшем будем записывать в приращениях переменных относительно их статических значений, вызванных постоянной массовой силой
Тогда уравнение (I.2.10) примет вид:
Тогда уравнение (I.2.10) примет вид:
Далее в тексте для удобства записи величину _____ будем обозначать через __ , а __ — через __ .
Уравнения (I.2.15) и (I.2.26) составляют связанную систему для описания совместного деформирования пористого скелета и фильтрации жидкости в нем:
Но поскольку для многих грунтов _____ , материал скелета можно считать несжимаемым:
Заметим, что полная производная ____ в этой формуле заменена на частную __ ввиду малости конвективной составляющей скорости изменения p. Обозначенная через ______ относительная сжимаемость воды имеет значение порядка
с коэффициентом сжимаемости _______ , дифференцированием по времени t получим:
Преобразуем (I.2.19) в уравнение для нахождения пористости:
Подставив в (I.2.18) выражения (I.2.20), (I.2.21), и закон Дарси, получим второе уравнение модели Био линейной фильтрации:
где ____ _ — начальные проницаемость и пористость, а текущая пористость n выражается через __ с помощью уравнения неразрывности.
Далее, предполагая отсутствие массообмена между жидкостью и скелетом, а также наличие источников (или стоков) жидкости с плотностью __ (размерность этой величины _____), запишем уравнение сохранения фазовых масс:
Далее, предполагая отсутствие массообмена между жидкостью и скелетом, а также наличие источников (или стоков) жидкости с плотностью __ (размерность этой величины _____), запишем уравнение сохранения фазовых масс:
Закон (I.2.16) может быть получен осреднением уравнений движения вязкой жидкости через поры линейно-упругого каркаса со стандартными условиями равенства напряжений и перемещений на поверхности раздела фаз.
В общем случае, тензор проницаемости __ зависит от эффективной объемной деформации твердой фазы
В общем случае, тензор проницаемости __ зависит от эффективной объемной деформации твердой фазы
уравнение (I.2.16) становится нелинейным. В качестве примера скалярной зависимости можно привести экспериментальную формулу:
Считая жидкость баратропной:
Фильтрация и консолидация — два ключевых процесса, определяющих поведение грунтов в различных инженерных задачах. Как предсказать осадку грунта или распределение порового давления? Как учесть влияние слоистой структуры при откачке жидкости? На эти и многие другие вопросы отвечает модуль FILTRATION, входящий в состав программного комплекса GeomechaniCS. Он предназначен для моделирования медленных процессов деформации пористых грунтов и течения насыщающей их жидкости под действием внешних сил.
Слои, поры и упругость: объект исследования
В рамках анализа рассматривается грунтовая толща со сложной слоистой структурой. Высокопористые водоносные слои чередуются с малопористыми, обладающими низкой водопроницаемостью.
Эти особенности требуют особого подхода к моделированию. В задачах фильтрации учитывается движение жидкости в поровом пространстве, а в задачах консолидации — уплотнение грунта и высачивание жидкости под действием внешних сил.
От Терцаги к Био: эволюция моделей
Первую модель совместного деформирования грунтов и насыщающей их жидкости предложил К. Терцаги. В рамках задачи консолидации он рассматривал водонасыщенный грунт как двухфазную среду и ввел понятие эффективного напряжения.
Основные характеристики модели Терцаги:
Модель Терцаги остается актуальной для задач, где горизонтальные деформации несущественны. Однако для более сложных условий требуется многомерный подход. Его предложил М. Био, разработав модель трехмерной консолидации.
Преимущества модели Био:
Как FILTRATION помогает инженерам?
Модуль FILTRATION в GeomechaniCS позволяет:
— Анализировать сложные системы слоистых грунтов
— Рассчитывать фильтрационные процессы с учетом изменения порового давления
— Оценивать осадки грунта в задачах консолидации
— Моделировать взаимодействие грунта и жидкости с высокой точностью
Использование современных моделей, таких как обобщение теории Био, делает этот инструмент незаменимым для проектирования сооружений в сложных геологических условиях.
Далее, мы подробно разберем математические основы модели, реализованной в модуле FILTRATION, и продемонстрируем ее практическое применение в инженерных задачах.
Модель грунтов, основанная на теории фильтрационной консолидации Био
Рассмотрим гетерогенную двухфазную среду в малом представительном объеме V. Эта среда состоит из твердой фазы — пористого или зернистого скелета (каркаса) — и жидкости, заполняющей поровое пространство между зернами.
Особенность структуры пор и зерен, характерная для различных типов грунтов, требует применения специального подхода. В модели Био используется теория смеси, позволяющая учитывать сложные взаимодействия между скелетом и жидкостью. В каждой точке исследуемого объема Vзадаются два основных параметра:
Слои, поры и упругость: объект исследования
В рамках анализа рассматривается грунтовая толща со сложной слоистой структурой. Высокопористые водоносные слои чередуются с малопористыми, обладающими низкой водопроницаемостью.
- Водоносные слои состоят из скальных пород (например, известняков), которые при умеренных нагрузках демонстрируют линейно-упругое поведение.
- Малопроницаемые слои обычно представлены глинами с мелкозернистой структурой. Несмотря на низкую пористость, это сильно сцементированные грунты, также подчиняющиеся законам линейной упругости.
- Поверхностный слой отличается рыхлой разрушенной структурой, которая уже при небольших нагрузках проявляет свойства неупругих материалов.
Эти особенности требуют особого подхода к моделированию. В задачах фильтрации учитывается движение жидкости в поровом пространстве, а в задачах консолидации — уплотнение грунта и высачивание жидкости под действием внешних сил.
От Терцаги к Био: эволюция моделей
Первую модель совместного деформирования грунтов и насыщающей их жидкости предложил К. Терцаги. В рамках задачи консолидации он рассматривал водонасыщенный грунт как двухфазную среду и ввел понятие эффективного напряжения.
Основные характеристики модели Терцаги:
- Одномерное описание процесса, учитывающее только вертикальные деформации
- Простота применения для расчета осадок поверхностных слоев
Модель Терцаги остается актуальной для задач, где горизонтальные деформации несущественны. Однако для более сложных условий требуется многомерный подход. Его предложил М. Био, разработав модель трехмерной консолидации.
Преимущества модели Био:
- Учет полного вектора перемещений в трехмерном пространстве
- Возможность моделирования процессов фильтрации и консолидации в слоистых грунтах
- Широкое применение в инженерной практике благодаря минимальному числу упрощений при сохранении физической достоверности
Как FILTRATION помогает инженерам?
Модуль FILTRATION в GeomechaniCS позволяет:
— Анализировать сложные системы слоистых грунтов
— Рассчитывать фильтрационные процессы с учетом изменения порового давления
— Оценивать осадки грунта в задачах консолидации
— Моделировать взаимодействие грунта и жидкости с высокой точностью
Использование современных моделей, таких как обобщение теории Био, делает этот инструмент незаменимым для проектирования сооружений в сложных геологических условиях.
Далее, мы подробно разберем математические основы модели, реализованной в модуле FILTRATION, и продемонстрируем ее практическое применение в инженерных задачах.
Модель грунтов, основанная на теории фильтрационной консолидации Био
Рассмотрим гетерогенную двухфазную среду в малом представительном объеме V. Эта среда состоит из твердой фазы — пористого или зернистого скелета (каркаса) — и жидкости, заполняющей поровое пространство между зернами.
Особенность структуры пор и зерен, характерная для различных типов грунтов, требует применения специального подхода. В модели Био используется теория смеси, позволяющая учитывать сложные взаимодействия между скелетом и жидкостью. В каждой точке исследуемого объема Vзадаются два основных параметра:

- вектор перемещения скелета , __ описывающий деформацию каркаса;
- давление жидкости p, отражающее состояние насыщения порового пространства.
Полное среднее напряжение ___ в такой среде:
определяется суммой осредненных микронапряжений в твердой и жидкой фазах:
Постановку задачи будем проводить, исходя из следующего предположения:
Для случая медленного течения жидкости, как это происходит при фильтрации, принято пренебрегать осредннным тензором вязких напряжений в жидкой фазе:
где p — осредненное давление, I — единичный тензор.
Введем понятие тензора эффективных напряжений
который интерпретируется как часть тензора средних напряжений ____ , обусловленная внешним макронагружением, а не давлением p в жидкости. Таким образом, полное напряжение из (I.2.2) и с учетом (I.2.5), можно представить в виде: ___ из (I.2.2) и с учетом (I.2.5), можно представить в виде:
Если поры каркаса не полностью насыщены жидкостью, а мерой насыщения является величина
Малая скорость фильтрации жидкости позволяет пренебречь инерционными слагаемыми в уравнениях движения фаз:
где ___ и ___ — плотность каркаса и жидкости, _— постоянная во времени массовая сила. Здесь и далее для частной производной по координате будем использовать обозначение:
Просуммировав уравнения (I.2.9), получим условие равновесия для полного напряжения
Предполагая, что для скелета выполняются соотношения линейной упругости, получим для:
где __ — эффективный тензор модулей упругости, __ — эффективные малые деформации.
Таким образом, ясен физический смысл тензора __ , как эффективной жесткости насыщенного грунта при нулевом давлении жидкости в порах.
Для связи деформаций __ с осредненными перемещениями твердой фазы __ воспользуемся соотношениями Коши для малых деформаций:
Для связи деформаций __ с осредненными перемещениями твердой фазы __ воспользуемся соотношениями Коши для малых деформаций:
Объединяя (I.2.11), (I.2.12) и (I.2.14), получим первое уравнение модели линейной фильтрации:
Для вывода второго уравнения модели воспользуемся законом Дарси, выражающим линейную зависимость относительной скорости жидкости __________ от градиента давления:
Здесь __ и __ — средние скорости жидкой и твердой фаз (точкой над символом обозначается частная производная по времени), __ — коэффициент динамической вязкости жидкости (измеряется в _____ ), а коэффициент __ (единицы измерения __ ) носит название тензора проницаемости каркаса. Уравнение (I.2.16) было экспериментально получено А. Дарси в 1856 году в опытах по течению жидкостей через цилиндрический слой песка для малых скоростей фильтрации.
Предел применимости данного закона в зависимости от относительной скорости течения жидкости в числах Рейнольдса: _________ . Закон Дарси часто также записывают в виде:
Предел применимости данного закона в зависимости от относительной скорости течения жидкости в числах Рейнольдса: _________ . Закон Дарси часто также записывают в виде:
Определяющие соотношения этого типа используются при описании деформирования твердых и полутвердых грунтов, примерами которых в геомеханике могут служить граниты и известняки. Для мягких грунтов, имеющих зернистую структуру (песчаный грунт или глина, например), линейные определяющие соотношения годятся лишь при небольших уровнях напряжений. В зависимости от напряжений, получаемых в задаче, может оказаться необходимым применять физически нелинейные уравнения состояния.
Однако в классе задач фильтрации под действием откачки (закачки) жидкости из скважины в слоистых грунтах использование закона Гука (I.2.12) оправдано геологической структурой грунта.
По смыслу самой задачи отбор жидкости осуществляется во флюидо-насыщенном слое, всегда состоящем из твердых или полутвердых пород, в которых давление откачки не вызывает больших деформаций. Данный водоносный слой, как правило, перекрыт верхним и нижним так называемыми «запирающими» слоями с малой пористостью и, соответственно, малой насыщенностью жидкостью. Это их свойство приводит к малым деформациям как в них самих, так и в оставшихся внешних слоях грунта, поскольку «запирающие» горизонты существенно снижают перепад давлений, вызванный работой насосов во флюидоносном слое. Поэтому деформации верхних мягких слоев грунта также можно достаточно точно описывать законом Гука.
Подставляя (I.2.12) в выражение для полного напряжения (I.2.7), получим:
Однако в классе задач фильтрации под действием откачки (закачки) жидкости из скважины в слоистых грунтах использование закона Гука (I.2.12) оправдано геологической структурой грунта.
По смыслу самой задачи отбор жидкости осуществляется во флюидо-насыщенном слое, всегда состоящем из твердых или полутвердых пород, в которых давление откачки не вызывает больших деформаций. Данный водоносный слой, как правило, перекрыт верхним и нижним так называемыми «запирающими» слоями с малой пористостью и, соответственно, малой насыщенностью жидкостью. Это их свойство приводит к малым деформациям как в них самих, так и в оставшихся внешних слоях грунта, поскольку «запирающие» горизонты существенно снижают перепад давлений, вызванный работой насосов во флюидоносном слое. Поэтому деформации верхних мягких слоев грунта также можно достаточно точно описывать законом Гука.
Подставляя (I.2.12) в выражение для полного напряжения (I.2.7), получим:
то добавив и вычтя из (I.2.2) член вида _____ получим выражение для __ в этом случае:
где ___ и ___ — объемы, занимаемые соответственно твердой и жидкой фазами, n — объемная пористость:
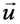
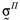
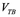
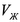
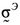

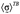
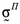
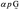
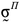




























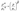
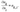
Здесь, как и в случае полного насыщения, __представляет собой полное напряжение в каркасе под действием совокупной внешней нагрузки при условии, что давление p равно нулю в той части объема пор, которая заполнена жидкостью. Коэффициент __ выражает отношение объема вытекшей жидкости к изменению объема пор скелета в случае, когда жидкость может беспрепятственно вытекать через поверхность тела. Таким образом, состоянию полного насыщения соответствует значение _____ , а отсутствию жидкости в порах — значение
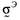
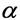
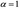

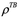
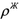
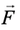
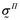

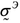
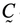
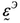
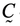
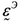
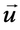
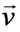
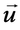
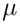
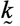
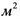
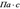



где __— тензорный коэффициент фильтрации жидкости, измеряемый в __, а _____ — вес
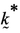

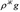

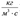
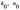

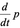
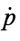
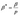

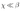
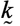
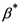
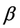
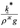
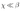
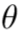
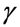
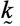
единицы объема жидкости.
Согласно предположению М. Био, сжимаемость зерен каркаса можно считать пропорциональной градиенту давления в жидкости:
откуда для уравнения (I.2.22) получим:
что, однако, не исключает объемные деформации твердой фазы в целом из-за наличия пор или возможности переупаковки зерен каркаса за счет их смещения. Поэтому окончательно второе уравнение модели линейной фильтрации с учетом условия (I.2.25) примет вид:
